Understanding Tim Sort

Author: Narendra Jha | Published on: Dec 28, 2019

Prerequisite: Insertion sort, Merge sort, and Quicksort

We know that Insertion sort works best when -
1. The input array is already partially sorted, and
2. The size of the input array is small
We also know that Merge sort's merge procedure works faster and better if the subarrays we are merging has size close to power of 2.

Now Tim sort uses above two properties of Insertion sort and Merge sort, and creates a hybrid of the two.

So Tim sort uses ideas from Insertion sort and Merge sort, and here is how it works -

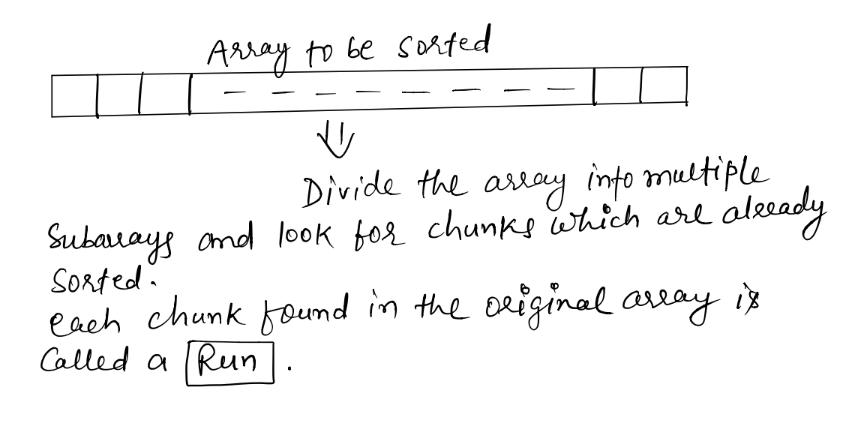
Now these Runs can be of any size, as sorted data in an input array can be found in any size.

The idea of Tim sort is based on the fact that real world input data often has this ordered chunks of data in it. It could be ordered in increasing or decreasing order. The idea is to merge the sorted chunks of data to get complete array sorted, and merging is done using merge procedure of Merge sort (so that is where Tim sort borrows idea from Merge sort)

Now the problem is, not everything in input array can be divided in ordered chunks of subarrays, as there will be portions in input array with random data in it, which is not sorted in any order, and that's where Insertion sort comes to rescue. The idea is to fix a minimum size of Runs (Subarrays that will be merged). Usually the minimum size of a Run is chosen as 64 or 32. Lets go with 64 size here. Let's call minimum size of a Run Minrun hereafter.

Minrun are chosen by keeping two things in mind -

Minrun should be small enough for Insertion sort to sort it faster, and
It should be close to power of 2, for merge procedure of Merge sort to work faster.

And that is why Minrun is often chosen as either 64 or 32.

Now we find this ordered sequence of data in input array, of sizes as close to Minrun (64) as possible, and then we take rest of the elements following it (or from either side of it), to complete a subsequence of size Minrun, and then we sort it using Insertion sort.

For example, if we find a subarray of size 24 which is already sorted in some order, then we take 40 more elements following it, and then Insertion sort it.

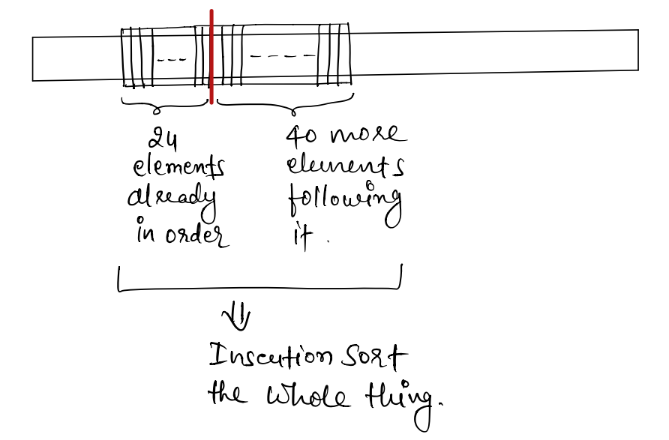
The protion of array which is already ordered, could be found ordered either in ascending or descending order, if ascending order - OK, if descending order - then we simply reverse it.

As stated earlier, Insertion sort works best when -

The input array is already partially sorted, and
The size of the input array is small

And both conditions here are met very well.
Some portion of the chunk we are sorting, is already sorted, and the size of Minrun (subarray) is 64 (or 32), which is small enough for Insertion sort to work very very fast.

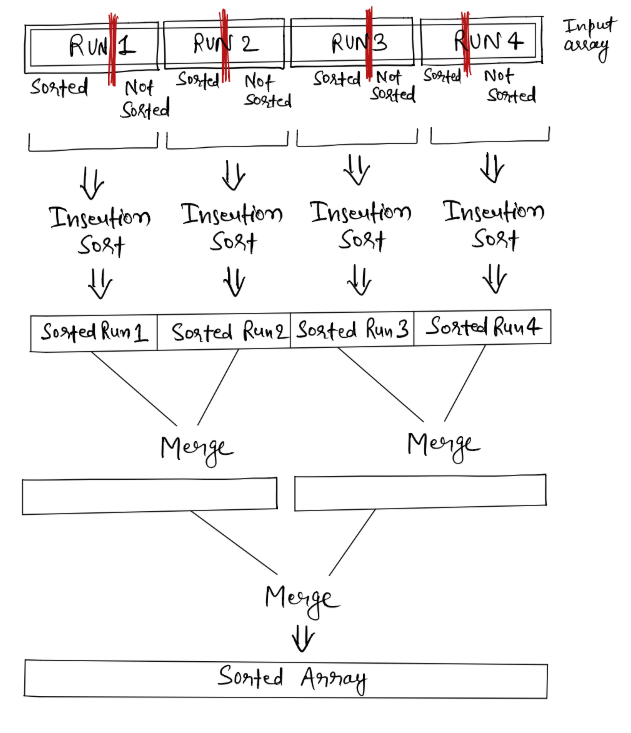
Now when we get a lot of these Runs which are sorted using Insertion sort, we merge them just like we merge sorted subarrays in Merge sort.

Time Complexity:

Best Case: O(n)
Average Case: O(n*lgn)
Worst Case: O(n*lgn)

Space Complexity: O(n)

Stability: Yes

Uses:

Tim sort is used in Python library
It is also used in Java 7.0 onwards for sorting non-primitive array or list. For sorting primitive array, Java uses Dual-Pivoted Quicksort

Timsort vs Quicksort:
When compared with Quicksort, Timsort has below advantages:

It is unbelievably fast for nearly sorted data sequence, and
The worst case is still O(n*lgn)

Quicksort's advantage over Timsort is that it works really fast for primitive array, because it utilizes processors memory caching abilities very well. It accesses a lot of near by elements, which can be accesses really really fast due to array's memory locality for primitive data.
For non-primitive data, arrays store addresses of objects, and actual objects are at different locations in heap section of memory, which makes accessing it slower compared to primitive data, which inturn makes the Quicksort algorithm slower, as it access a lot of near by elements.

Checkout Python and Java's library implementations of Timsort.

Further reading :
hackernoon.com/timsort-the-fastest-sorting-algorithm-youve-never-heard-of-36b28417f399
en.wikipedia.org/wiki/Timsort
medium.com/@rylanbauermeister/understanding-timsort-191c758a42f3

Feel free to shoot your questions at njha.sde@gmail.com